Lab 5: Intro to automatic differentiation and PyTorch

This notebook is intended to introduce:

• the basic ideas of automatic differentiation and how to use it in PyTorch;

• the basic ideas of PyTorch and how to use it to train a simple MLP.

Installation

Follow the instructions on the PyTorch website to install PyTorch. We will only use the CPU version in this lab, so you can ignore the CUDA related options.

PyTorch basics

PyTorch can be used as a replacement of Numpy

import numpy as np
import torch

M1 = np.array([[1., 2., 3.], [4., 5., 6.]])
M1

array([[1., 2., 3.],
       [4., 5., 6.]])

M1.shape

(2, 3)

v1 = np.array([1., 2., 3.]).reshape(3, 1)

v1

array([[1.],
       [2.],
       [3.]])

M1@v1

array([[14.],
       [32.]])

M2 = torch.tensor([[1., 2., 3.], [4., 5., 6.]])
M2

tensor([[1., 2., 3.],
        [4., 5., 6.]])

M2.shape

torch.Size([2, 3])

v2 = torch.tensor([1., 2., 3.]).reshape(3, 1)

M2@v2

tensor([[14.],
        [32.]])

Converting between numpy and torch

torch.from_numpy(M1)

tensor([[1., 2., 3.],
        [4., 5., 6.]], dtype=torch.float64)

M2.numpy()

array([[1., 2., 3.],
       [4., 5., 6.]], dtype=float32)

Automatic differentiation with PyTorch

We will use the following simple example to illustrate the basic ideas of automatic differentiation.

\(L = (y - wx)^2\)

\(\frac{\partial L}{\partial w} = 2(y - wx)(-x)\)

\(\frac{\partial L}{\partial x} = 2(y - wx)(-w)\)

x = torch.tensor([1., 2., 3.])
w = torch.tensor([4., 5., 6.], requires_grad=True)
y = torch.zeros(3)

diff =  y - w*x
diff

tensor([ -4., -10., -18.], grad_fn=<SubBackward0>)

square = diff**2
square

tensor([ 16., 100., 324.], grad_fn=<PowBackward0>)

L = torch.sum(square)
L

tensor(440., grad_fn=<SumBackward0>)

Get the gradient of L with respect to w

# dw = torch.autograd.grad(L, w)

# dw

Cannot get grad of L with respect to x (because x does not require grad)

# dx = torch.autograd.grad(L, x)

Alternative way to get grad instead of calling autograd.grad

Note:

• this is the recommended way to get the gradient.

• cannot backpropagate a second time. So comment out the above dw cells to run the below.

L.backward()

w.grad

tensor([  8.,  40., 108.])

print(x.grad)

None

You can even get higher order derivatives

def get_loss(w):
    x = torch.tensor([1., 2., 3.])
    y = torch.zeros(3)

    L = torch.sum((y - w*x)**2)

    return L

Get the Hessian

from torch.autograd.functional import hessian

w = torch.tensor([4., 5., 6.], requires_grad=True)

hessian(get_loss, w)

tensor([[ 2.,  0.,  0.],
        [ 0.,  8.,  0.],
        [ 0.,  0., 18.]])

MLP with PyTorch

import torch.nn as nn

class MyTwoLayerMLP(nn.Module):

    def __init__(self, num_input_nodes, num_hidden_nodes, num_out_nodes):
        super().__init__()

        self.num_input_nodes = num_input_nodes
        self.num_hidden_nodes = num_hidden_nodes
        self.num_out_nodes = num_out_nodes

        self.linear1 = nn.Linear(num_input_nodes, num_hidden_nodes)
        self.linear2 = nn.Linear(num_hidden_nodes, num_out_nodes)



    def forward(self, X):

        h = self.linear1(X)
        h = torch.relu(h)
        y = self.linear2(h)

        return y

Let’s create some data to test our model

torch.manual_seed(0)  # random seed

def generate_data(N, num_in=3):
    """Generate some random data with num_in=3 features x1, x2, x3.
    The target is y = x1^2 + x2^2 + x3^2.

    Args:
        N: number of samples
        num_in: number of input features
    """
    X = torch.randn(N, num_in)
    y = torch.square(X).sum(dim=1).reshape(N, 1)

    return X, y

X, y = generate_data(N=100, num_in=3)

X.shape

torch.Size([100, 3])

y.shape

torch.Size([100, 1])

Create a model with 10 hidden nodes

num_in = 3
num_hidden = 10
num_out  = 1

model = MyTwoLayerMLP(num_in, num_hidden, num_out)

Let’s check that the model works

y_pred = model(X)

y_pred.shape

torch.Size([100, 1])

Train the model

def train_one_step(model, optimizer, X, y):
    """Performs one step of gradient descent on the given model.

    Args:
        model: the model to train
        optimizer: the optimizer to use
        X: the input data
        y: the target data
    """
    y_pred = model(X)
    loss = torch.mean((y_pred - y)**2)

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    return loss

### Using SGD optimizer
optimizer = torch.optim.SGD(model.parameters(), lr=0.001)

num_steps = 30

losses = []
for s in range(num_steps):
    for X_i, y_i in zip(X, y):
        l = train_one_step(model, optimizer, X_i, y_i)
        losses.append(l.item())

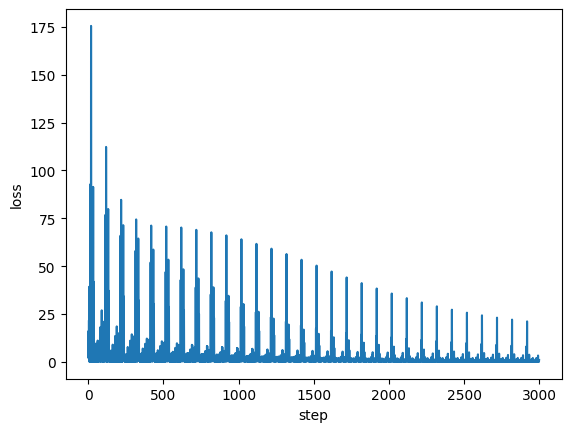
import matplotlib.pyplot as plt

fig, ax = plt.subplots()

ax.plot(losses)

ax.set_xlabel('step')
ax.set_ylabel('loss')

# Note, the loss is the training loss for each individual sample

Text(0, 0.5, 'loss')